BQ#7

Q. Explain in detail where the formula for the difference quotient comes. 

The difference quotient formula comes from a formula that we know very well since the beginning of our high school career. The formula y2-y1/x2-x1. With this formula is where it all started.on a curved graph we use variables to distinguish the unknown points . With the midpoint formula we bring.together the variables

BQ #6 Unit U

1. What is a continuity?
A continuity is a graph that we can draw without lifting our pencil off the paper. It has  no holes jumps or breaks. The value and limit are the same.

Examples:

B) What is a discontinuity?
 There are two discontinuity families:removable and non removable discontinuities.A removable discontinuity is a point discontinuity which is known as a hole.Then we have a jump discontinuity in which the graph looks like it jumps lower i.n the coordinate plane. An oscillating graph looks wiggly because the graph is going up and down so many times we can see it. Finally we have an infinite graph that that results in unbounded behavior near a vertical asymptote.

Examples :

Jump discontinuity

                      Infinite discontinuity

Oscillating discontinuity

2) What is a limit?
A limit is the intended height of the graph. In other words its the height the graph wants to reach but doesn't actually reach it.

B) When does a limit exist?
A limit exists  when the function intends to reach its certain intended height. A limit usually exists with a point discontinuity.

C) When does a limit not exist?
There are 3 situations that a limit doesn't exist; jump,oscillating and infinite discontinuity.
A limit doesn't exist for a jump discontinuity because it "jumps" on the plane. The term its different from the left and right tells us it doesn't have a limit. Then an oscillating graph doesn't have a limit because it has oscillating behavior meaning we can see how many times the graph goes up and down. Finally, an infinite discontinuity doesn't have a limit because of unbounded behavior. The graph goes in opposite directions for infinity.Thos happens when we have a.vertical asymptote.

BQ # 2 Unit R

How do the trig graphs relate to unit
Circle?

A. Why Is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi.

For a sine graph we know that sine is.postive.in the first to.quadrants and negative in quadtants 3and 4. Cosine is positive then negative, its a pattern that goes on forever. 2pi is how long it takes for each pattern to repeat itself. We are unwrapping the unit circle into a straight line.




A tangent and cotangent

BQ #3

How do the graphs of sine and cosine relate to each of the others?

Tangent

In a tangent graph,we relate to the identity of tan equals sin /cos. Cos equals zero and this will tells us where it will lie on the graph.

BQ 5

Why do sin and.cosine nit have asymptotes, but the other four trig graphs do?

Asymptotes are undefined. Sjne and cosine dont have demoninators that equal zero. Sine has the ratio y/r and cosine has a ratio of x/r. In the unit circle r equals 1. Therefore we will always get a value. The other four trig graphs have a possibility of getting value a of zero.

BQ #4 unit R

Why is the period for sine and cosine 2 pi,whereas the period for tangent and cotangent is pi?


The trig graph is a unit circle that is unwrapped. For sine ans cosine, 2pi is how long it takes for the graph to repeat itself.



For tangent and cotangent pi is how long it takes to repeat itself

reflection#1 unit Q Verifying trg identities.

To verify a trig function means to prove the left side if it is correct while not touching the right side. We must prove it is correct because we use our identities to prove them right.

2.I had to memorize the identities because this is what will help us throughout the unit. Another tip.is to.look for identities that we can replace with and have the same . Like sin for the whole equation

3.I start by looking at the left side . I dont touch the right side. We look if we can substitute a identity or reciprocal. We get a a common denominator or gcf. We do all we need to get our answer on the left. This includes several key factors that will help us achieve our proven equation.

Sp#7 Unit Q

“This SP7 was made in collaboration with William de Leon_.  Please visit the other awesome posts on their blog by going williamdperiod5.blogspot.com

I/D #3 unit Q

Where does sin2x+cos2x=1 come from to begin with (think Unit Circle!). You should be referring to Unit Circle ratios and the Pythagorean Theorem in your explanation.

An identity is any proven facts and formulas tht are always true. We have the unit circle in which we have our magic 5  pair. We get sin2x +cos2x =1. If we get any value on the unit circle like radical 3/2,1/2.if we do the math we end up getting the overall answer to equal 1



Inquiry reflection activity.


If I had to describe trigonometry in THREE words, they would be…

Wpp#13/14 unit p

This WPP13-14 was made in collaboration with  Damian Gomez and William de leon.  Please visit the other awesome posts on their blog by going    To damiangperiod5.blogspot.com And willaimdleonperiod5.blogspot.com

BQ #1 Unit P

Law of Sines - Why is SSA ambiguous?
 
The ambiguous case occurs when one uses the law of sines to determine missing measures of a triangle when given two sides and an angle opposite one of those angles. In some cases we have zero,one or two solutions. I such cases we assume that there are two possible triangles and we know we are done when we hit a wall. 

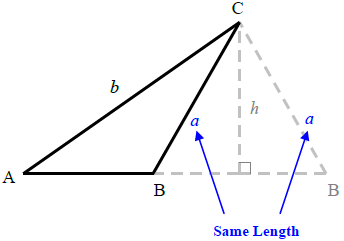
The above picture is an example of a one possible solution triangle. As we can see that it gives us two sides and one angle. We first start by finding the missing angles. We use the law of sine to find the "bridge" to the other triangle. Its usually the the same side and angle.


Area formulas - How is the “area of an oblique” triangle derived?  How does it relate to the area formula that you are familiar with?

The area of an oblique triangle is derived by having two side and one angle. 


REFERENCE


http://www.gradeamathhelp.com/law-of-sines.html

WPP #12 Unit 0 concept 10

Wall jump

A)  A man wants to jump a wall from the ground. The angle of elevation is 25 degrees 21 minutes. If the base of the wall is 32 feet away from the man, how tall is the wall?

B) The same man now stands atop the wall. He measures the angle of depression to be 26 degrees 2 minutes from a hole in the ground. He knows that he is 27 feet higher than the base. How long is the hole?

                                    A

B

I/D1: Unit O - Derive the SRTS

1.Inquiry Activity Summary

For this activity we are asked to find how to the srt of special right triangles. We see that we are given that the side us equal to 1.We are able to get the values that is the formula. We see that the variable n is in a relationship with all sides that have a connection together.





O
We have an equilateral triangle whose sides equal 1. For us to get the sides ,we have to cut the triangle in half . It gives us a 30,60,90 triangle. We see what we have and notice right away that one side of the triangle is split in one half . So we have two 1/2's and a 1 side We can use the Pythagorean theorem to help gwt the other values.




Inquiry Activity Reflection

Something I never noticed before about special right triangles I that the triangle value works for any triangle that has limited information.

I/D1: Unit N - How do SRT and UC relate?

INQUIRY ACTIVITY SUMMARY







* 30 degree  triangle description







A 30 degree angle is close to the x axis and it is closer to zero on a coordinate plane.the 30 degree triangle has a the same coordinate as as 60 degree triangle.The 30-60-90 triangle is the only right triangle whose angles are in an arithmetic progression. A 45 degree angle is half of a right angle and is on the middle of the first quadrant.We have a 30 degree triangle that its special rules are 2x,x radical 3, and x. in the directions we are told that r is equal to 1. Therefore we are left with 2x,x radical 3, and x. In order for us to have R (hypotenuse)equal to 1 we have to divide by 2x to all sides.The r side is 1 then x radical 3 divided by 2x is radical 3 over 2.The last side is x divided by 2x is 1/2. I was able to get the 30 degree angle coordinates for the unit circle.This lies in the 1 quadrant.

*60 degree triangle description


 
 A 60 degree angle is close to the x axis.We have a 60 degree triangle that its special rules are 2x,x radical 3, and x. in the directions we are told that r is equal to 1. Therefore we are left with 2x,x radical 3, and x. In order for us to have R (hypotenuse)equal to 1 we have to divide by 2x to all sides.The r side is 1 then x radical 3 divided by 2x is radical 3 over 2.The last side is x divided by 2x is 1/2. I was able to get the 60 degree angle coordinates for the unit circle.This lies in the 1 quadrant.





* 45 degree  triangle description

This is a 45-45-90 triangle whose special rules are 2x,x radical 2 ,x radical 2. We are given that r is equal to 1. We divide everything by 2x. We get 1, radical 2 over 2 ,radical 2 over 2.

 INQUIRY ACTIVITY REFLECTION
1. The coolest thing I learned from this activity was… that every coordinate is located on the unit circle. I never knew that we can use this to get a value of a given point.

 2. “This activity will help me in this unit because i need to learn the unit circle by memory and i need to be able to do it quick. I also need to know this to do well on the test and be able to pass the test. 

3.Something I never realized before about special right triangles and the unit circle is they are identical and they are the ones that are all over the circle.I see that it is the same for all other quadrants.

RWA #1 Unit M

1.Mathematical definition PARABOLA-the set of all points the equidistant from a point called the focus and a line called the directrix.(Mrs. Kirch) 2.Mathematical equation-(x-h)^2=4p(y-k) and (y-k)^2=4p(x-h) Graphically x-h The directrix is the line that crosses the vertex.the focus located on the directrix line. 3. This picture shows how parabolas are are used in real life.they are mathematically calculated to be kept standing and to support a roof. Its interesting how a simple shape can cause the building to stand. Parabolas are seen in buildings and bridges. It requires equations that help the engineer built a stable building or bridge. For bridges it must be calculated to be strong enough to hold cars. 4.www.chelsfield.com/project/the-parabola/ www.mathwarehouse.com/geometry/parabola/real-world-application.php

Wpp 10 Unit L Concept 9-14

Create your own Playlist on LessonPaths!

Wpp 9 :Unit L Concept 9

Create your own Playlist on LessonPaths!